Curvas cúbicas de Bézier
Para dibujar una curva de Bézier en el <canvas> utilizamos, además de otros métodos()
y propiedades ya conocidas, un método especifico: bezierCurveTo()
| JavaScript | Descripción | Defecto | |
|---|---|---|---|
| lineWidth | context.lineWidth = numero; | Determina (sets) o devuelve (returns) la grosor de la línea. | 1 |
| strokeStyle | context.strokeStyle = color | gradient | patrón; | Determina (sets) o devuelve (returns) el color, gradiente o patrón de la línea. | negro |
| fillStyle | context.fillStyle = color | gradient | patrón; | Determina o devuelve el color, gradiente o patrón del relleno. | negro |
| beginPath() | context.beginPath(); | Empezamos a dibujar | |
| bezierCurveTo() | context.bezierCurveTo(cx1,cy1,cx2,cy2,x,y); | Define una curva de Bézier. cx1,cy1,cx2,cy2= coordenadas puntos de anclaje P1 y P2 (control points) x,y = coordenadas punto final P3 (el punto de partida siendo determinado previamente). |
|
| fill() | context.fill(); | Rellena una forma geométrica. | black |
| stroke() | context.stroke(); | Dibuja una línea ya definida. |
Vea la chuleta con las propiedades y metodos() de canvas.
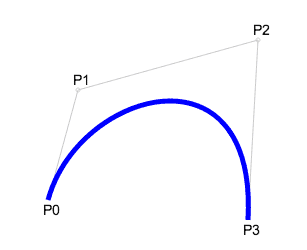
Repaso de Geometría
Cuatro puntos del plano: P0, P1, P2 y P3 definen una curva cúbica de Bézier.
La curva empieza en el punto P0, se dirige hacia P1 y llega a P3 viniendo de la dirección del punto P2.
Usualmente, no pasará ni por P1 ni por P2. Estos puntos sólo están ahí para proporcionar información direccional.
See the Pen 53f7f0ff953dbb5799be66c887102663 by Gabi (@enxaneta) on CodePen.
Lea más sobre las curvas de Bézier en Wikipedia
Veamos un ejemplo. A continuación dibujamos una curva de Bézier en el <canvas>. Utilizamos ctx.moveTo(x0,y0) para mover el "lapiz"
en el punto P0. Para esbozar la curva utilizamos ctx.bezierCurveTo(x1,y1,x2,y2,x3,y3), donde x1, y1 son las coordenadas del punto P1, etc...
Para dar estilo a la curva utilizamos como siempre las propiedades lineWidth y strokeStyle. Al final dibujamos la curva con stroke().
ctx.beginPath();
ctx.moveTo(x0,y0);
ctx.bezierCurveTo(x1,y1,x2,y2,x3,y3);
ctx.stroke()
Visite cubic-bezier.com (Made by Lea Verou with care). Verá un maravilloso ejemplo de curvas de Bézier, realizado con <canvas>.
var canvas = document.getElementById("lienzo");
if (canvas && canvas.getContext) {
var ctx = canvas.getContext("2d");
if (ctx) {
var x0 = 20; var y0 = 160;
var x1 = 50; var y1 = 50;
var x2 = 230; var y2 = 0;
var x3 = 220; var y3 = 180;
ctx.lineWidth = 5;
ctx.strokeStyle = "#00f";
ctx.beginPath();
ctx.moveTo(x0,y0);
ctx.bezierCurveTo(x1,y1,x2,y2,x3,y3);
ctx.stroke();
}
}Calcular las coordenadas de un punto en la curva
Para calcular las coordenadas de un punto en la curva de Bézier utilizamos una fórmula encontrada en Wikipedia
var x = (1 - t) * (1 - t) *(1 - t) * x0
+ 3 * (1 - t) * (1 - t) * t * x1
+ 3 * (1 - t) * t * t * x2
+ t * t * t * x3;
var y = (1 - t) * (1 - t) *(1 - t) * y0
+ 3 * (1 - t) * (1 - t) * t * y1
+ 3 * (1 - t) * t * t * y2
+ t * t * t * y3;
El paámetro t ( var t ) es muy importante. Puede tomar valores entre 0 y 1 y representa la posición del punto en la curva.
Si t == 0, el punto se encuentra al inicio de la curva, coincidiendo con x0, y0.
Si t == .5 el punto cuyas coordenadas queremos calcular se encuentra justo en el medio de la curva.
Si t == 1 el punto se encuentra al final de la curva, coincidiendo con x3, y3.
var canvas1 = document.getElementById("lienzo1");
if (canvas1 && canvas1.getContext) {
var ctx1 = canvas1.getContext("2d");
if (ctx1) {
var x0 = 20; var y0 = 160;
var x1 = 50; var y1 = 50;
var x2 = 230; var y2 = 0;
var x3 = 220; var y3 = 180;
ctx1.lineWidth = 5;
ctx1.strokeStyle = "#00f";
ctx1.beginPath();
ctx1.moveTo(x0,y0);
ctx1.bezierCurveTo(x1,y1,x2,y2,x3,y3);
ctx1.stroke();
//calculamos las coordenadas del punto
var t = .7; // toma valores entre 0 - 1
var x = (1 - t) * (1 - t) *(1 - t) * x0
+ 3 * (1 - t) * (1 - t) * t * x1
+ 3 * (1 - t) * t * t * x2
+ t * t * t * x3;
var y = (1 - t) * (1 - t) *(1 - t) * y0
+ 3 * (1 - t) * (1 - t) * t * y1
+ 3 * (1 - t) * t * t * y2
+ t * t * t * y3;
// dibujamos un punto rojo
ctx1.beginPath();
ctx1.fillStyle = "red";
ctx1.arc(x,y,10,0,2*Math.PI);
ctx1.fill();
}
}